Arrays are one of the most fundamental data structures in computer science. But did you know that Python doesn't have a built-in array data type? Instead, Python provides a versatile data structure called a list. Let's find out what the difference is between Python lists and traditional arrays, and the under the hood operations that make Python lists so efficient.

Programming languages including C, C++, and Java provide built-in support for arrays. They share the following characteristics:

1) Homogeneous data storage:

Arrays store elements of the same data type. This means all elements in an array must me integers, floats, characters, or objects of the same class.

2) Index-based access:

Elements in an array are accessed using an integer index. The index typically starts at 0 and goes up to n-1, where n is the size of the array.

3) Fixed size at creation:

In many programming languages, arrays have a fixed size that must be defined when the array is created.

a = new int[10];
 
a[0] = 1;
a[1] = 20;
a[9] = a[0] + a[1];

The size cannot be changed after initialization without creating a new array.

4) Constant-time element access:

One of the most powerful features of array is that they allow constant-time O(1) access to any element, regardless of the array's size. This is possible because the memory address of any element can be calculated using the base address of the array and the index of the element.

address_of(a[i]) = address_of(a[0]) + i * size_of(a[0])

5) Contiguous memory allocation:

Arrays are stored in contiguous blocks of memory. This means that all elements are stored next to each other, which enables efficient access and traversal like we saw in the previous point.

To understand how arrays work at a low level, it's important to grasp some basics of computer memory architecture.

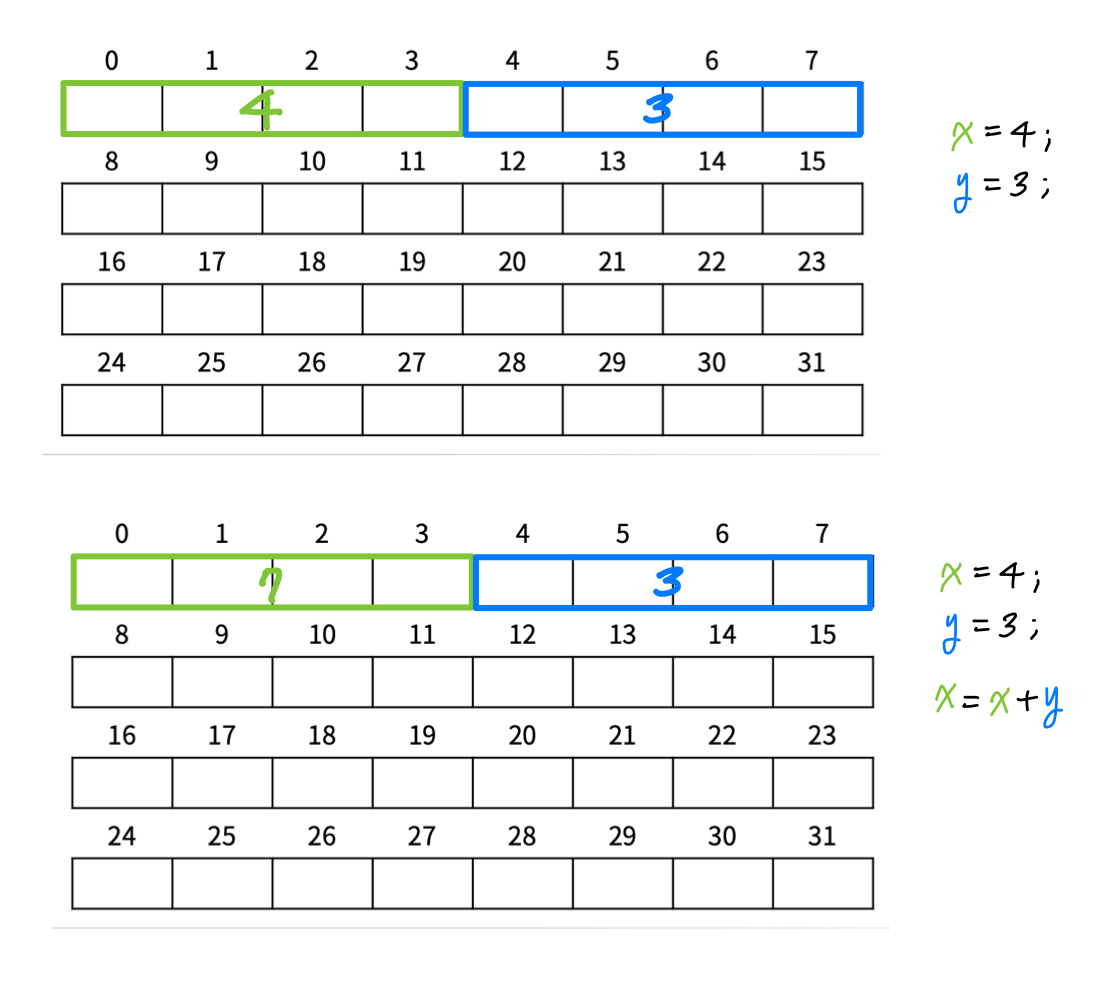
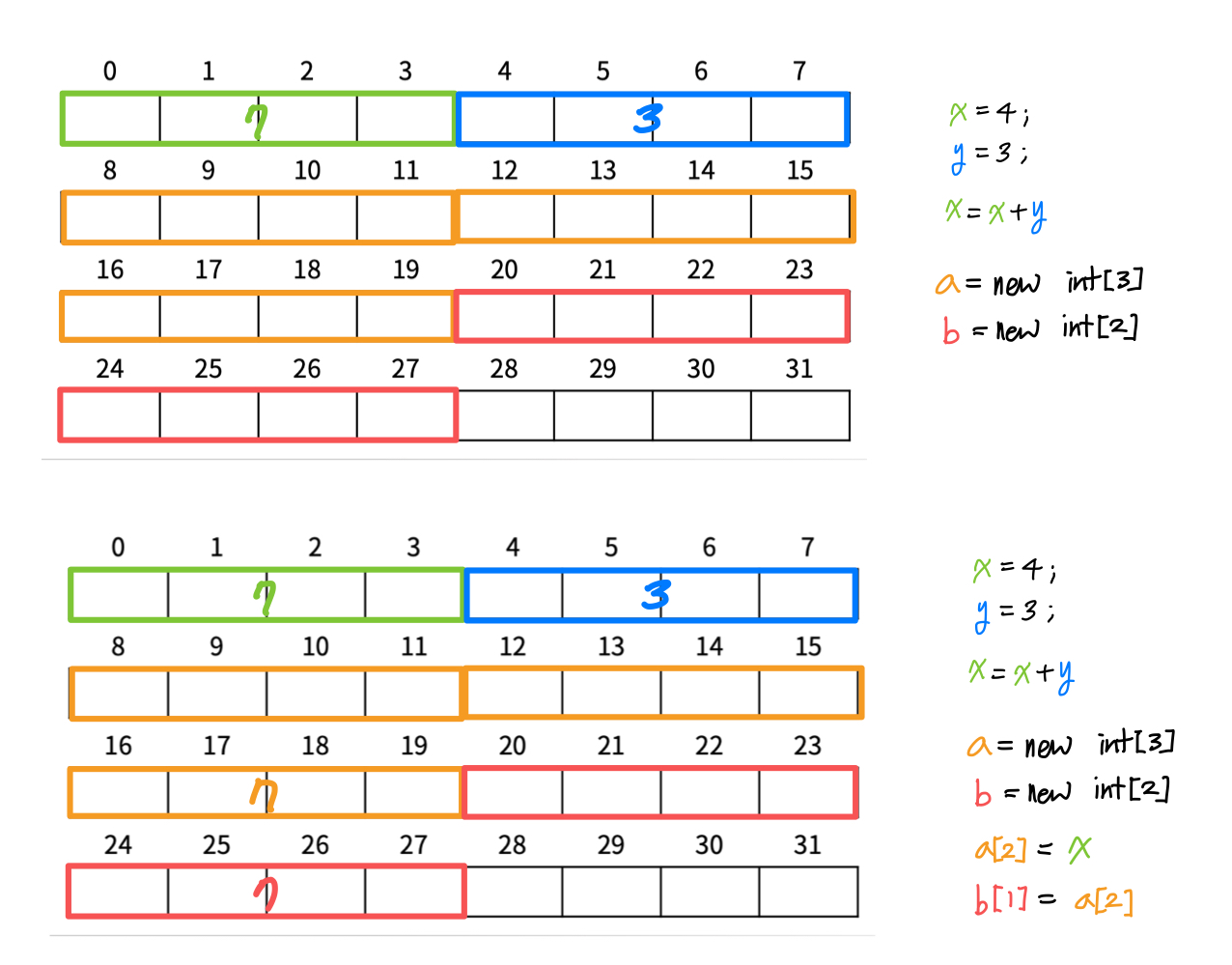
1) Byte-addressable memory:

Computer memory is organized into bytes, each with unique address. (1 byte = 8 bits)

2) Address-based memory access:

When a program needs to access data in memory, it uses memory addresses to locate the data. For arrays, the address of any element can be calculated using the base address of the array and the element's index.

3) Role of interpreters/compilers in memory management:

It's the interpreter/compiler's job to figure out the address where each variable is stored.

The way arrays are handled in memory can vary depending on the programming language and whether it uses a compiler or interpreter. For example:

• In compiled languages like C and C++, array access is translated directly into memory address calculations.
• In interpreted languages like Python or JavaScript, there's an additional layer of abstraction. The interpreter manages memory allocation and access, often implementing arrays as more complex data structures behind the scenes.

Similarities:

• Index-based access: Like arrays, Python lists allow for direct access to elements using integer indices.
• Constant-time element access: Like arrays, accessing elements by index in a Python list is an O(1) operation. This is because Python lists maintain an internal array of pointers to the actual objects stored in the list.
• Contiguous memory allocation

Differences:

The key difference between Python lists and traditional arrays lies in their dynamic sizing capabilities. Unlike fixed-size arrays, Python lists can grow or shrink dynamically as needed. You can add or remove elements without worrying about pre-allocating memory or running out of space.

But is it possible to have a contiguous memory allocation with dynamic sizing? I mean what if I wanna add something to a list but there's already something in the memory block?

Python resolves this paradox through a smart technique which is memory reallocation.

Memory reallocation process:

• A new, larger block of memory is allocated.
• All existing elements are copied from the old block to the new block.
• The old block is freed.

This process is actually can be done by other languages as well, but the key difference is that in other languages, developers should handle this process manually while in Python, it's done automatically.

At first glance, one might expect the time complexity of n append operations to be θ(n^2), considering the worst-case scenario where each append triggers a reallocation. However, the actual performance is much better.

Expected θ(n^2) complexity:

If every append operation required a reallocation and copy, we would indeed see quadratic time complexity.

Actual O(n) complexity:

In reality, the over-allocation strategy ensures that reallocations occur much less frequently, leading to a linear time complexity for n append operations.

To understand the true efficiency, we need to consider amortized analysis.

Amortized analysis considers the average performance of a sequence of operations, rather than focusing on the worst-case scenario fo each individual operation. This approach provides a more realistic view of the data structure's performance in practice.

Case study: appending 1025 elements

What if Python gives memory 2 times bigger than the current size when it needs to reallocate?

Let's consider appending elements 1025 times.

Total execution time

The total time for n append operations can be expressed as:

T(n) = n * (cost of simple append) + Σ(cost of reallocations)

The sum of reallocation costs can be approximated as O(n), leading to an overall linear time complexity.

Amortized cost per operation

By dividing the total cost by the number of operations, we find that the amortized cost per append operation is O(1). This means that, on average, each append operation takes constant time.

In conclusion, Python's list implementation cleverly resolves the paradox between fixed memory and dynamic sizing through over-allocation and efficient reallocation strategies. While individual operations may occasionally be expensive, the amortized performance ensures that lists remain highly efficient for most use cases, providing both the benefits of contiguous memory access and the flexibility of dynamic sizing.